Perl Contains the Lambda Calculus
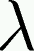
(How to write a 163 line program to compute 1+1)
Length: 90 minutes
Prerequisites: None.
Description
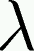 -Calculus
(pronounced `lambda calculus') is a model of computation invented by
Alonzo Church in 1934. It's analogous to Turing machines, but it's
both simpler and more practical. Where the Turing machine is
something like a model of assembly language, the
-Calculus
(pronounced `lambda calculus') is a model of computation invented by
Alonzo Church in 1934. It's analogous to Turing machines, but it's
both simpler and more practical. Where the Turing machine is
something like a model of assembly language, the 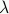 -calculus is a model of
function application. Like Turing machines, it defines a
simplified programming language that you can write real programs in.
Writing Turing machine programs is like writing in assembly language,
but writing
-calculus is a model of
function application. Like Turing machines, it defines a
simplified programming language that you can write real programs in.
Writing Turing machine programs is like writing in assembly language,
but writing 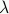 -calculus programs is more like writing in a higher-level
language, because it has functions.
-calculus programs is more like writing in a higher-level
language, because it has functions.
The two legal operations in the 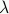 -calculus are to construct a function of one
argument with a specified body, and to invoke one of these functions
on an argument. What can be in the body of the function? Any legal
expression, but expressions are limited to variables, function
constructions, and function invocations. What can the argument be?
It has to be another function; functions are all you have. With this
tiny amount of machinery, we can construct a programming language that
can express any computation that any other language can express.
-calculus are to construct a function of one
argument with a specified body, and to invoke one of these functions
on an argument. What can be in the body of the function? Any legal
expression, but expressions are limited to variables, function
constructions, and function invocations. What can the argument be?
It has to be another function; functions are all you have. With this
tiny amount of machinery, we can construct a programming language that
can express any computation that any other language can express.
Unlike most popular programming languages, Perl is powerful enough
to express the 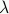 -calculus directly, without the need to write a
simulator. This means that if you want to try programming in the
-calculus directly, without the need to write a
simulator. This means that if you want to try programming in the 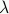 -calculus, you can do it
directly in Perl, without having to implement a program to parse and
evaluate
-calculus, you can do it
directly in Perl, without having to implement a program to parse and
evaluate 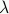 -calculus
expressions first. Perl's parser will parse
-calculus
expressions first. Perl's parser will parse 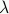 -expressions, if you write them properly,
and its evaluator will evaluate them.
-expressions, if you write them properly,
and its evaluator will evaluate them.
In the 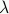 -calculus,
a function with formal parameter x and body B is denoted
-calculus,
a function with formal parameter x and body B is denoted 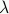 x.B. In Perl, we
write sub { my $x = shift; B }.
x.B. In Perl, we
write sub { my $x = shift; B }.
To apply the function P to an argument Q, the usual
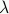 -calculus notation
is just (P Q). In Perl, we write $P->($Q).
-calculus notation
is just (P Q). In Perl, we write $P->($Q).
The only expressions not of either of these two forms are simple
variables. To apply the function 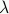 v.B to some argument A is simple. The
result is just B, but with any occurrences of v replaced
with A instead. For example (
v.B to some argument A is simple. The
result is just B, but with any occurrences of v replaced
with A instead. For example (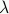 x.(x (x y))(P Q)) reduces to ((P
Q) ((P Q) y))---we replaced all the x's with (P
Q)s.
x.(x (x y))(P Q)) reduces to ((P
Q) ((P Q) y))---we replaced all the x's with (P
Q)s.
By convention, function application is taken to be
left-associative, so that (P Q R) is short for ((P Q)
R).
From these few materials we can construct a programming system capable
of performing arithmetic, constructing lists and trees, and expressing
arbitrary recursive functions on these objects.
Complete Slides
- Perl and the Lambda Calculus
- What is the Lambda Calculus?
- Turing Machine
- Turing Machines
- Lambda-Calculus
- Lambda-Calculus
- Abstraction
- Application
- Application Example
- Application
- Abstraction Again
- Goal
- Values
- Church-Rosser theorem
- Undefined Values
- Currying
- Currying
- Boolean Values
- Boolean Value Example
- Boolean Value Example
- Data Structures
- Ordered Pairs
- Ordered Pair Example
- Ordered Pair Example
- Numbers
- Number Example
- Arithmetic
- Recursion
- Fixed Points
- o For any _f_,
- Y = IMG:lambda-6.gif:_f_.(IMG:lambda-6.gif:_x_.(_f_ (_x_ _x_)) IMG:lambda-6.gif:_x_.(_f_ (_x_ _x_)))
- Return from Digression
- OK, We're Done
- Building an Interpreter
- There's a Catch
- Applicative Order Solution
- Applicative Order Solution
- IMG:lambda-4.gif:-Calculus in Perl
-
Additional Materials
- Runnable Perl source code:
- If you're familiar with
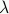 -calculus, but not with Perl, read the article that I submitted to the Journal of Functional Programming.
-calculus, but not with Perl, read the article that I submitted to the Journal of Functional Programming.
- If you're familiar with Perl, but not with the
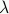 -calculus, read this other article instead. (Caution: Still in draft stage.)
-calculus, read this other article instead. (Caution: Still in draft stage.)
Return to:
Universe of Discourse main page |
Perl Paraphernalia |
Other Classes and Talks
mjd-perl-yak+@plover.com
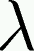 -Calculus
(pronounced `lambda calculus') is a model of computation invented by
Alonzo Church in 1934. It's analogous to Turing machines, but it's
both simpler and more practical. Where the Turing machine is
something like a model of assembly language, the
-Calculus
(pronounced `lambda calculus') is a model of computation invented by
Alonzo Church in 1934. It's analogous to Turing machines, but it's
both simpler and more practical. Where the Turing machine is
something like a model of assembly language, the 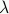 -calculus is a model of
function application. Like Turing machines, it defines a
simplified programming language that you can write real programs in.
Writing Turing machine programs is like writing in assembly language,
but writing
-calculus is a model of
function application. Like Turing machines, it defines a
simplified programming language that you can write real programs in.
Writing Turing machine programs is like writing in assembly language,
but writing 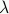 -calculus programs is more like writing in a higher-level
language, because it has functions.
-calculus programs is more like writing in a higher-level
language, because it has functions.