| Next | Continued Fraction Arithmetic | 46 |
This is probably the most important property of continued fractions
Suppose you truncate the continued fraction for n
You get a very good rational approximation for n
In fact, you get the best possible rational approximation for n
(In the sense that no fraction with a smaller denominator is closer)
Consider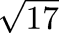 
= [4; 8, 8, 8, 8, ...] = 4.12310562561...:
[4] = 4/1 = 4
[4; 8] = 33/8 = 4.125
[4; 8, 8] = 268/65 = 4.1230769...
[4; 8, 8, 8] = 2177/528 = 4.12310606
[4; 8, 8, 8, 8] = 17684/4289 = 4.123105619...
268/65 has a denominator smaller than 4.12 = 412/100
But it is more than 100 times as accurate
Even 33/8 is more accurate than 412/100
Conclusion: You needn't calculate the whole expansion of a continued fraction
If you stop early, you get a good approximation
| Next | Back |