Bricolage: Data Compression
© Copyright 1998 The Perl Journal. Reprinted with permission.
 You are probably familiar with Unix
You are probably familiar with Unix compress, gzip, or bzip2
utilities, or the DOS pkzip utility. These programs all make files smaller; we say that such files are compressed. Compressed files take less disk space and less network bandwidth. The
downside of compressed files is that it they are full of unreadable
gibberish; you usually have to run another program to uncompress them before you can use them again. In this article we'll see how file
compression works, and I'll show a simple module that includes functions
for compressing and uncompressing files.
The idea behind data compression is very simple. In a typical file, say a
text file, every character takes up the same amount of space: 8 bits. The
letter e is represented by the 8 bits 01100101; the letter Z is represented by the 8
bits 010101010. But in a text file,
e occurs much more frequently than Z---maybe about 75 times as frequently. If you could give the common symbols
short codes and the uncommon symbols long codes, you'd have a net gain.
This isn't a new idea. It was exploited by Samuel Morse in the Morse Code,
a very early digital data transmission protocol. Morse Code was designed to
send text files over telegraph wires. A telegraph is very simple; it has a
switch at one end, and when you close the switch, an electric current
travels through a wire to the other end, where there is a relay that makes
a click. By tapping the switch at one end, you make the relay at the other
end click. Letters and digits are encoded as sequences of short and long
clicks. A short click is called a
dot, and a long click is called a dash.
The two most common letters in English text are E and T; in Morse code these are represented by a single dot and a single dash,
respectively. The codes for I, A, N, and M, all common letters, are **, *-, -*, and --. In contrast, the codes for the uncommon letters Q and Z are --*- and --**.
In computer file compression, we do a similar thing. We analyze the
contents of the data, and figure out which symbols are frequent and which
are infrequent. Then we assign short codes to the frequent symbols and long
codes to the infrequent symbols. We write out the coded version of the
file, and that usually makes it smaller.
There's a problem with Morse Code: You need a third symbol, typically a
long pause, to separate the dots and dashes that make up one letter from
the dats and dashes that make up the next. Otherwise, if you get
*-, you don't know whether it's the single letter A or the two letters ET---or it might be the first bit of the letter R or L. In a long message, all the dots and dashes run together and you get a big
mess that can't be turned back into text. In Morse code, it can be hard to
tell `Eugenia' from `Sofia': Without the interletter pauses, they're both:
***---**-****-
Those interletter spaces take up a lot of transmission time, and it would
be nice if you didn't need them. It turns out that if you arrange the code
properly, you don't. The ambiguity problem with Morse Code occurs because
some codes are prefixes of others: There are some letters where the code for the first part of one
letter is just the same as the code for the other letter, but with
something extra tacked on. When you see the shorter code, you don't know if
it's complete or if it should be combined with the following symbols. It
turns out that if no code is a prefix of any other, then the code is
unambiguous.
Suppose for simplicity that we only needed to send the letters A, C, E, and
S over the telegraph. Instead of Morse code, we could use the following
code table:
A -
C **
E *-*
S *--
Suppose we receive the message -*****-**--*--*-**--. What
was the message? Well, the first symbol is -, so the
first letter in the message must be A, because that's the
only letter with a code that starts with a -. Then the
next two symbols are **, so the second letter must be a
C, because all the other codes that start with
* have a - after the * instead
of another *. Similar reasoning shows that the third
letter is also C. After that, the code is
*-*; it must be an E. We continue through
the message, reading off one letter at a time, and eventually we get
the whole thing this way.
It's so simple that a computer can decode it, if the computer is equipped
with a decision tree like this one:
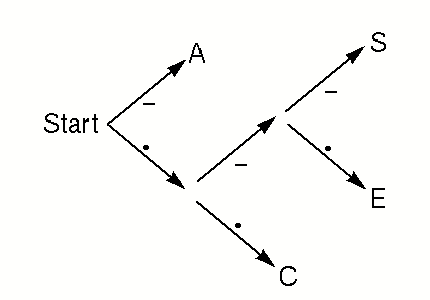
Start at Start, and look at the symbols in the message one by one. At each stage, follow
the appropriate labelled branch to the next node. If there's a letter at
that node, output the letter and go back to the start node. If there's no
letter at the node, look at the next symbol in the input and continue down
the tree towards the leaves.
Obviously, it's important to choose the right code. If Morse had made
the * code for Z and **-* the
code for E, he wouldn't be famous.
Choosing the right code can be tricky. Consider the example of the
previous section, where we only had to code messages that contain
A, C, E, and S.
The code I showed is good when we expect our messages to contain more
A's than E's or S's. If
S were very common, we clearly could have done better;
less clearly, if all four letters were about equally common, then we
could still have done better, by assigning each letter a code of the
same length:
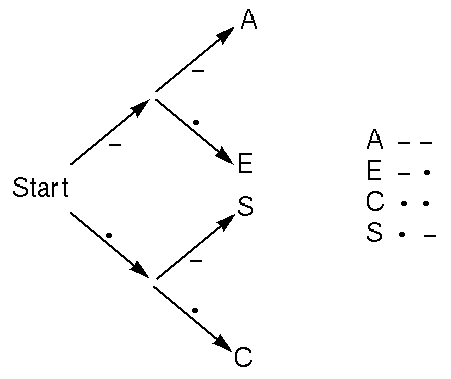
Suppose, for example, our message happened to contain 200 of each of the
four letters. Then the first code would use 1800 symbols, and the second
code would use only 1600.
In 1952, David Huffman discovered a method for producing the
optimal unambigous code. For a given set of symbols, if you
know the probability with which each symbol appears in the input, you
can use Huffman's method to construct an unambiguous code that encodes
the typical message with fewer *'s and -'s than any other code.
The method is very simple and ingenious. For concreteness, let's suppose
that the (rather silly) message is
THE_THIRSTIEST_SISTERS_TEETH_RESIST_THIS_STRESS
(I used _ instead of space so that it'll be easier to see.)
Start with the table of relative probabilities; you can get this by
counting the number of occurrences of every symbol in the message. This is
called histogramming. (A histogram is a bar chart;
histos is Greek for a beam or a mast.) Here's the histogram for the symbols in our
sample message:
| S | 11 |  |
| T | 10 |  |
| E | 7 |  |
| _ | 6 |  |
| I | 5 |  |
| H | 4 |  |
| R | 4 |  |
Now take the two least common entries in the table, that's
H and R. They'll get the longest codes,
because they're least common. We'll simplify this by pretending that
H and R are the same, and lumping them
together into one category, which we'll call HR. Then
we'll assign codes to all the other letters and to
HR. When we're done, we still have to distinguish between
H and R. Now, HR has some
code. We don't know what it is yet, so let's symbolize it with
<HR>. We don't really need to use
<HR> in our message, because the is no such thing
as the letter HR, so we'll split it in two, and let the
code for H be <HR>* and the code for
R be <HR>-. As a result of this, the
codes for H and R will be longer than the
codes for the other letters, but if that has to appen, it's better for
it to happen for H and R, because they are
the least common letters in the message.
So we will lump H and R together and pretend temporarily that they are only
one letter. Our table then looks like this:
S 11 R = <HR>-
T 10 H = <HR>*
HR 8
E 7
_ 6
I 5
Now we repeat the process. The two least common symbols are
I and _. We'll lump them together into a new
`symbol' called I_, we'll assign finish assigning the
codes to S, T, HR,
E, and I_. When we're done, I
will get the code <I_>* and _ will get
the code <I_>-.
S 11 R = <HR>-
I_ 11 H = <HR>*
T 10 _ = <I_>-
HR 8 I = <I_>*
E 7
Then we lump together HR and E:
HRE 15 R = <HR>-
S 11 H = <HR>*
I_ 11 _ = <I_>-
T 10 I = <I_>*
HR = <HRE>-
E = <HRE>*
Then we lump together T and I_:
I_T 21 R = <HR>-
HRE 15 H = <HR>*
S 11 _ = <I_>-
I = <I_>*
HR = <HRE>-
E = <HRE>*
I_ = <I_T>-
T = <I_T>*
Then we lump together S and HRE:
SHRE 25 R = <HR>-
I_T 21 H = <HR>*
I = <I_>-
_ = <I_>*
HR = <HRE>-
E = <HRE>*
I_ = <I_T>-
T = <I_T>*
S = <SHRE>-
HRE = <SHRE>*
Now we only have two `symbols' left. There's only one way to assign a
code to two symbols; one of them gets * and the other
gets -. It doesn't matter which gets which, so let's say
that SHRE gets * and I_T gets
-.
Now the codes fall out of the table we've built up in the right-hand
column:
SHRE = *
S = *-
HRE = **
HR = **-
R = **--
H = **-*
E = ***
I_T = -
I_ = --
_ = ---
I = --*
T = -*
We throw away the codes for the fictitious compound symbols, and we're left
with the real code:
S = *-
T = -*
E = ***
_ = ---
I = --*
H = **-*
R = **--
As promised, the code is unambiguous, because no code is a prefix of any
other code. Our original message encodes like this:
-***-****----***-*--***--*--*--*****--*---
*---**--******--*-----*******-***-*---
**--****---**--*----***-*--**----
*--***--****-*-
For a total of 128 *'s and -'s, an average of 2.72 symbols per character,
and a 9.3% improvement over the 141 symbols we would have had to use if we
had given every letter a three-symbol code.
For this article, I implemented a demonstration module that compresses
files. You can retrieve it from the perl Journal web site at http://www.tpj.com/ or from my Perl
Paraphernalia web site at http://www.plover.com/~mjd/perl/Huffman/.
The program htest.pl
compresses an input and saves it to the file /tmp/htest.out; then it opens this file, reads in the compressed data, decompresses it,
and prints the result to standard output.
Most of the real work is in the Huffman module that htest uses. Here are the important functions that htest calls:
my $hist = Huffman::histogram(\@symbols);
This generates the histogram of the input text. The histogram is the tally
of the number of occurrences of each symbol. The argument to
histogram is an array of symbols, passed by reference for efficiency, because it is
likely to be very large. It might have been simpler to pass the input as a
single string, but this way we can assign codes per-word instead of
per-character if we want to, just by splitting the input into an array in a
different way.
my $codes = Huffman::tabulate($hist);
The tabulate function generates the code table from thie histogram using Huffman's
method. (This has the side effect of destroying the histogram.) The code
table is just a hash that maps symbols to codes; the codes themselves are
strings like 0010011.
Huffman::save_code_table(*FILE, $codes);
This writes the code table to the file.
Huffman::encode(*FILE, $codes, \@symbols);
This encodes the input text and writes the result to the file.
my $codes = Huffman::load_code_table(*FILE);
my $coded_data = <FILE>;
my $text = Huffman::decode($codes, $coded_data);
This is the decompression process. The return value from
load_code_table is a code table in a rather interesing form. It's a decision tree, just
like the ones we saw earlier in the article. Each node of the tree is
either a single string (which is the symbol that the decoder should output)
or it's an array with two elements; the 0th element is the part of the tree
on the branch labeled 0, and the 1st element is the part of the tree on the
branch labeled 1. For example, taking * as equivalent to 0 and - as
equivalent to 1, the decision tree from earlier in the
article would be represented like
this:
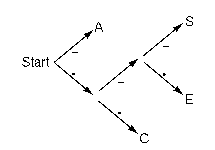
[[C,
[E,
S
]
],
A
]
We can compress the file, but unless we include the code table in the
compressed file, we won't be able to uncompress it again. Files that
can't be uncompressed are not very useful. (Sometimes you don't need
to be able to decompress the file; in these cases the Perl
unlink function implements a much simpler and more
efficient form of compression.) But sometimes the code table is
bigger than the savings that we got from compressing the file,
especially if the original file is small. On a sample file of
comp.lang.perl.misc articles, the compressor reduced the file
size by 32%, from 42733 bytes to 29114. But when I ran it on its own
source code, the file size increased from 987 bytes to 1321. The
compressed data was only 631 bytes long, but the code table and other
overhead took up 690 bytes.
Huffman coding is optimal in the sense of compressing a given set of
symbols into the smallest space possible. But if you readjust your idea of
a `symbol', you can get must better compression.
Suppose you're compressing English text. If you histogram the characters,
and use Huffman's method, you'll get the optimal way to encode the
characters. Because each character has its own code, your code would also
serve to code arbitrary random gibberish. It should be clear that this
expressiveness has a price. For English text, we don't need so much
expressiveness; it's clearly more efficient to assign a code to each word instead of to each character. In doing so, we lost the ability to encode
random gibberish, but our compressed data becomes much smaller. Suppose
there are about 2**17 words in English; if we assign each one a different
17-bit code, we can then encode our original seven-word message:
THE THIRSTIEST SISTERS TEETH RESIST THIS STRESS
into 7*17 = 119 bits, alreasy an improvement on the 128 we used before. And
if we use Huffman's method to assign long codes to rare words and short
codes to common words, we can do even better.
Using this method, I compressed the comp.lang.perl.misc articles by 63%. Unfortunately, the code table blew up as a result, and
took up 43739 bytes, which was larger than the original uncompressed data.
Most modern data compression doesn't use Huffman coding directly. A better
method was proposed in 1977 and 1978 by Jakob Ziv and Abraham Lempel. The
Lempel-Ziv methods scan the input data, and when they find a substring that
occurs twice, the replace the second occurrence with a reference back to
the first. The references can then be Huffman-compressed.
These methods have several advantages over the basic scheme I implemented.
One important benefit of Lempel-Ziv compression methods is that they don't
have to read and analyze the entire input in advance; they can construct a
code table as they go along, basing it on only the portion of the input
seen so far. This is important for practical applications. The data
compression in your modem wouldn't be very useful if the modem had to
gather and analyze a week's worth of traffic before it could send or
receive anything.
Another benefit of this method is that because the code table is
imlpicit in the input seen so far, the code table doesn't need to be
recorded explicitly. The decoding process can infer the code table
from the coded data itself. This avoids the embarrassing inflamations
that we saw where the code table took up more space than was actually
saved by the compression process.
One extra payoff of building the code table on the fly is that if
the algorithm notices that the code table it's using isn't performing
well, it can throw it away and start over in the middle. If the data
is in several pieces that have very different characters, say a
graphic image embedded in a text file, this method will be a win over
straight Huffman coding because it'll be able to apply an appropriate
code table to each part of the data. LZW, the compression algorithm
used by the DOS lha program, doesn't do this, but the
variation of it employed by the Unix compress program
does. The algorithm used by the GNU project's gzip and
zlib is different but also periodically throws away the
code tables and starts over.
The best thing about Lempel-Ziv and related methods is that they don't need
to decide in advance how to break up the input into symbols. LZW, for
example, puts any string that it hasn't seen before into the code table,
under the assumption that if it appeared once, it'll probably appear again.
As the input comes in, longer and longer substrings of the input go into
the code table; long substrings go in only when their shorter prefixes have
appeared multiple times. This means that if the file is best broken up into
words, the algorithm will eventually detect that; if it is best broken up
into single characters, the algorithm will detect that too.
If you want an easy but possibly amusing project, try altering
the code table functions in the module so that the code tables
are smaller. At present, the module does not assume that
the coding is done per-character, so you shouldn't break that.
Actually, though, assigning the codes per-word seems to blow
up the code table more than it saves. I haven't found a case
yet where it's worthwhile. I'd be interested in seeing more
analysis of this.
Finally, the decision-tree data structure in the decoder is
probably over-clever. It would be simpler to represent the
same information with a state table, this way:
0 1
--------------------
0 1 A
1 C 2
2 E S
Each internal node in the decision tree is assigned a state,
which is a number; the root node gets the number 0. To
decode, the decoder keeps track of the state number, which
says what internal node it's currently at. Each time it reads
a bit, it looks in the table to decide where to go next. If
it sees a symbol, that means it erached a leaf, and should
output that symbol and start over at state 0; if it sees a
number, that means it's now at a different internal node and
should read more bits. I'm really not sure whether this would
be more efficient than the way I did do it, but it would
probably be easier to understand.
Symbols, Signals, and Noise, J.R. Pierce, pp. 94--97. Harper, New York, 1961.
The comp.compression FAQ, is an excellent starting source of information,
especially part 2. It is available from ftp://rtfm.mit.edu/pub/usenet/news.answers/compression-faq/.
My column finally has a name! Bricolage is a hot word these days in the computer learning business; it's French for tinkering or
pottering. Thanks to Deven Ullman, who suggested it, and to the other people who
suggested other names.

Return to:
Universe of Discourse main page |
What's new page |
Perl Paraphernalia|
File Compression Page
mjd-tpj-huffman@plover.com
 You are probably familiar with Unix
You are probably familiar with Unix 


