
I wrote this talk for Recurse Center and gave it on Monday, 20 April 2015.
As I get better at giving talks, the talk slides capture less and less of the actual material. These are lecture notes from what I said that evening.
Libby Horacek and Chris Ball came to my dress rehearsal and helped me clarify unclear points beforehand. Libby supplied me with notes about what needed to change. Chris arranged to video the talk when I gave it that evening. My sincere thanks to both.
Rachel Vincent, the Recurse Center ops manager, told me what sort of talk to prepare. But I had a tough time picking an actual topic and I spent a while thrashing around to figure out something that both made me a better programmer and was technical. Most of the things I thought of that made me a better programmer are not technical. Stuff like, stop and contemplate for a few minutes before writing any code. Although I could give a decent talk on that, it wasn't what was asked for.
By far the most important thing that made me a better programmer was, in fact, blood, toil, tears, and sweat. To the extent that I'm good at this, it's that I have been practicing almost every day for thirty years, constantly learning new techniques, new systems, new languages, analyzing past errors critically, evaluating my own practices, and always trying to connect together everything I know.
But it wasn't “of a technical nature”.

A talk about Structure and Interpretation of Computer Programs would have been great, and it is certainly the most important book on programming that I have ever read. I spent about three years studying it. But all that studying was done twelve or fifteen years ago, and it is now so deep inside me that I don't know any more which parts are me and which are SICP. I could have written a great talk about it, if I had had time to go back, reread the book, and remind myself what were all the things I learned from it. But I didn't have time to do that.
Every day I write some code, and then I say “Well, this is so simple I don't need to write any tests for it.”
Then a voice in my head says “Just write the tests, fool!” And I do, and the tests find seven bugs.
For me, writing the tests is like looking both ways when I cross the street: not something I should decide to do, but something I should do every single time without deciding.
But it wasn't sufficiently technical.
If I hadn't read The Unix Programming Environment by Kernighan and Pike when I was twenty, I don't even know who or what I would be now. It completely altered the path of my life. The Unix “tools” approach, where you build a powerful system made of small interchangeable parts, is the essential component of my design philosophy. It's the reason for my interest in functional programming which has driven so much of my career.
And Unix itself made me a better programmer because it is a platform designed by programmers to support programming, and it supports me in a million tiny but crucial ways, every single day.
But everyone at the talk would already be familiar with Unix, and I didn't want to give a talk where I just reminded people of things they already knew.

I'm not actually sure that bourbon has made me a better programmer, although I don't think it has hurt.
But it wasn't sufficiently technical.
When I thought of hashes, I knew I had found a winner. One of the tricky things about the audience was that it was very mixed, including beginning programmers as well as grizzled experts. I could explain to the newbies how hashes worked, explain to the Perl and Python folks how Perl and Python differed, and lay some strange and interesting history on people who knew all the technical parts already.
“Around 1980ish” here refers to AWK, which is the earliest language I know about that has real hashes, and was the direct inspiration for the hashes in Perl and Python.
I couldn't find out when Lisp symbols acquired property lists (plists), but it must have been very early. These are lists, not hashes, but you think about them roughly the same way, although they don't scale.
SNOBOL, I must emphasize, is nothing at all like COBOL; its name is a joke. SNOBOL was developed between 1963 and 1967 and was an incredibly forward-looking language. But the future to which it looked was not the future we actually live in, so it remains innovative even today! SNOBOL had, in 1967, a better pattern-matching system than Perl has now. SNOBOL had (non-hash) associative data structures, called “tables”, twelve years before Awk. We will see SNOBOL tables in detail later.
Awk was the breakthrough, the first language of which I am aware that had lightweight, dynamic hash tables.
REXX is also of some interest. Nobody in the room knew REXX, which
was originally developed for IBM's “CMS” operating system for
mainframes, and then had a strange reincarnation as the principal
scripting language for the Amiga microcomputer. It had a hashlike
feature where you could subscript a variable, say foo, with a
suffix, say foo.bar, and that was a new variable.
Lightweight hashes finally reached their full flowering in Perl (1987) and Python (1990).
Standard arrays map numeric indices to arbitrary data.
Hashes map strings to arbitrary data.
Arrays have been in programming since day 1. They are intrinsic to the way memory is laid out in a computer. They are as fast as anything can possibly be. To look up an array element given the index requires a multiplication, an addition, and a fetch.
Hashes are trickier to do but still very old, dating back to the early 1950s. You cannot have an entry for every possible string, so you need some way of translating the strings to actual storage locations.
Some languages allow hash keys to be any type of data, not just strings. They do this by translating the key to a string behind the scenes. For example, if you wanted to use an object as a hash key, the system might make up a key by concatenating a special prefix, the object's class, and its storage address.
All data inside the computer is ultimately strings, when viewed at the right level, so something like this is always possible. The details are only a matter of performance tuning.
Although syntax varies from system to system, hashes always support a store operation, where a given value is associated with a given key; if another value was previously associated with that key, the old association is discarded. They always support a fetch operation, where the value associated with a given key is looked up.
Hashes also support a "contains" operation, which asks if there is a value associated with a given key. This isn't necessary for arrays, where there is an association for a given index if and only if the index is in range for the array.
Hashes usually support an operation to retrieve a list of all the keys. Again this isn't necessary for arrays, because you can generate the ‘keylist’ with simple counting.
Since the hash might have millions or billions of keys, you don't always want to allocate memory to store a list of all of them at once. So there is often an iterator interface which gets the keys in order, one at a time.
Slide 12 slide neglects to mention deletion. That is an oversight.
Slide 13 shows how some of these operations look in Perl and in Python.
Slide 14 adds Condoleezza Rice, who is not impressed with your petty complaints about Perl's syntax.

It can be hard to remember now, but hashes changed everything.
Alfred North Whitehead said that civilization advances by extending the number of important operations which we can perform without thinking about them. I'm not sure that's true, but if you replace “civilization” with “programming” I agree completely. With the introduction of hashes that you don't have to think about, all sorts of difficult things became easy and impossible things became possible.
Slide 16 shows a completely mundane and typical example: We have some
blogging platform, and it is going to read a bunch of article files
and assemble the contents into a web page. There is a
handle_article callback that is called repeatedly, once for each
article on the page. It is passed the article's unique filename, the
article's category (“math”, “sports”, “kids”, whatever) and the file
contents. It gathers these and then composes the right articles into
a page. That part is already written.
We now want to modify the callback to also accumulate a count of the number of articles in each category, so that we can generate a tag cloud or something. How do we do this?
Prior to hashes, we would have to actually do some programming. But
with hashes, it's nearly a one-line change. We allocate a hash
variable to map categories to counts, and each time through
handle_article, we increment the count associated with the current
article's category.
Slide 17 explains a desideratum I didn't mention: sometimes the blog
software is called upon to generate several pages at once. Sometimes
the same article appears on several pages. In this case,
handle_article is called multiple times for the same article, and
counts its category each time, so the totals are wrong.
Prior to hashes, we would have to actually do some programming. But with hashes, it's nearly a two-line change. On slide 18 we allocate another hash, to record which articles have been counted already, mapping their unique paths to booleans. For each article, we check to see if it's already in the hash. If not, we count its category as before, and mark it has having been seen already. Next time we see the same article, we know to skip it.
Not too well! The easiest way to construct an association structure is with a linked list, and this was frequently done, because it is so easy.
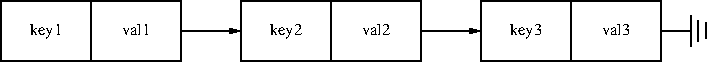
I give pseudocode for a linked-list implementation, which would be
easy enough to translate to C. The only tricky point is that the
first argument to store must be passed by reference so that store
can modify it to include a new key-value pair. (This can be avoided
with another indirection: all functions get a pointer to a cell that
contains a pointer to the head of the list.)
If you are sufficiently dedicated, you can even implement this in a language like Fortran that does not have dynamic memory, but that is a top for another talk that I hope I will never give.
Slide 20 gives one noteworthy example of the linked-list approach from
the language Lisp, which has done this since sometime in the 1960s.
(I think. I was not able to find an exact date. But it must have
been a long time ago, because the fetch function is called get and
not get-property-list-associated-value.) In Lisp this structure is
sometimes called an assoc list and sometimes a plist (short for
‘property list’.) The only difference from the slide 19 version is
that Lisp keeps the keys and values in alternating conses.
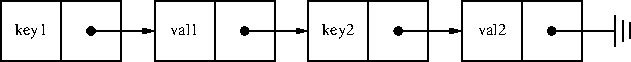
But once you find the key, then you cake the cadr of that cell and
you have the associated value.
The big drawback of assoc lists should be apparent: not only the worst-case but the average case for fetch and store require O(n) time. To create a list with n items requires quadratic time, because each time you must search the list, looking in vain for the key you are about to insert. and the list is longer each time.
How can we fix this? The first thing that comes to mind is to use trees instead of lists. Trees typically have O(log n) search time to inserting n items requires only O(n log n) time.
Unfortunately, the worst case for trees is O(n) also, and this worst case comes up frequently in practice. If the keys are inserted into the tree in alphabetical order, or reverse alphabetical order, or something close, you get a tree that is very tall and stringy, nothing but a list, pretending to be a tree, and it is even slower to search than the corresponding list would have been.
There are a lot of workarounds for this. For example, 2–3 trees (slide 22), where you insert items at the bottom and if the tree gets overfull, some of the items percolate up toward the top and the tree gets less unbalanced. Or red-black trees (slide 23), which are like 2-3 trees except that when you have a node that should have two keys and three children you simulate it with two nodes instead. Or (slide 24) my all-time least favorite data structure, the self-balancing AVL tree, where you notice when the tree gets unbalanced and rearrange it to balance things out.
The principal use of most of these things seems to be to torment undergraduate CS students taking classes in Algorithms and Data Structures. Useless crap like this is why I was not a CS major.
(I should put in a good word for 2-3 trees, which are nothing but a special case of the very practical and important B-tree structure.)
In contrast to trees, hashes have better average-time behavior. They have the same worst-case behavior, namely O(n) fetching and storing. But, unlike trees where there worst-case behavior is easily triggered by the very common case of pre-sorted data, the worst case of a hash only appears at random, and with vanishingly small probability. I mean that in a formal mathematical sense. For a large hash to hit the worst case requires either actual malice or an impossibly large dose of bad luck, akin to being hit by a meteor on the way to collect your lottery jackpot. Unless your hash is actually being attacked, you can ignore it, the same way you ignore meteor strike risk. And if the attacks are a concern, they are easy to defend against anyway.
I wasn't sure where to slip this in but it was too interesting to leave out. Like Lisp, SNOBOL has an associative data structure, this time called a ‘table’. Unlike Lisp, the table was not a linked list.
In SNOBOL, there is a single giant hash table, not pictures on this slide, whose keys are every single string that exists in the entire program. Strings include string values and also variable names. When you write something like
NAME = 'HAMILTON'
SNOBOL first calculates the string NAME and looks for it in the
giant hash table, creating an entry for it, if it is not already
there, with a pointer to a fresh, empty variable structure. It then
does the same for HAMILTON, again creating a fresh, empty variable.
Then it installs a the pointer to the second structure into the first
structure, so that the value of NAME is HAMILTON.
Because of this SNOBOL can perform unusual operations: You can write
VAR = 'NAME'
$VAR = 'HAMILTON'
which is equivalent to the assignment above: VAR contains the name
of the variable into which HAMILTON is stored, and it could be
computed via an arbitrarily complicated expression.
I glossed over the crucial point here. In most languages, if you write
A = 'HAMILTON'
B = 'HAMILTON'
you get two unrelated HAMILTON objects, one stored in A and one in
B. Not so in SNOBOL. When the second string is constructed, SNOBOL
finds the HAMILTON in the giant hash table from the first assignment
and stores an identical pointer into the variable B. The two
variables point to the same thing.
But suppose you then mutate B. Doesn't that mutate A also? Say
we add a star to the end of B:
B = B '*'
Does A change? No, at that time SNOBOL consults the giant hash
table, looking for HAMILTON*, creates a new entry for it if there is
none already, and stores the pointer to that structure into B,
leaving A pointing to the old HAMILTON structure.
SNOBOL's associative data structure is called a “table’. Slide 26
depicts a table that associates the value MARGARET with HAMILTON,
as created by the assignment
T<'HAMILTON'> = 'MARGARET'
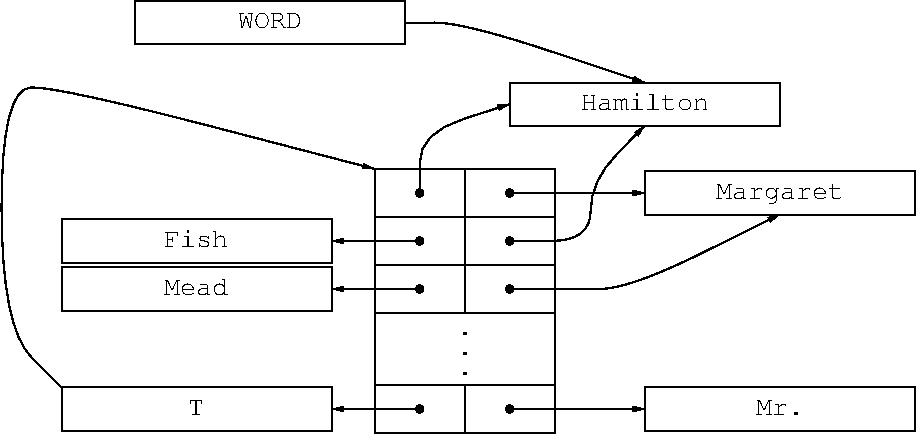
The table is essentially an array with two columns, one for the keys
and one for the values. SNOBOL first searches the giant hash table
for a string HAMILTON, creating one if necessary and yielding a
pointer to its unique structure, which is stores in the left-hand
column. Then it does the same thing for MARGARET, storing the
pointer in the right-hand column.
Now suppose we want to extend the table with T<'FISH'> = 'HAMILTON'.
(Hamilton Fish was Governor of New York in the 1870s.) SNOBOL searches
the giant table for FISH and finds or creates that string and
installs a pointer to it in the left side of the table. Then it
searches the giant hash for HAMILTON, finding the exact same object
that it found last time, and installing the same pointer on the
right.
Now suppose we want to search the table looking for FISH. SNOBOL
first finds FISH in the giant hash and produces the unique pointer
to it. It then scans the left-hand column looking that exact pointer.
This, of course, is O(n), but it is the fastest possible O(n), because each step requires only a single pointer comparison: because strings are unique, if the pointer matches, the string is found, and if not then it is some other string. So each comparison requires a single machine instruction, and that is going to beat a more complex algorithm unless the table is very large.
But the table can't be that large because computers don't have that much memory in 1965! BAHAHAHA!
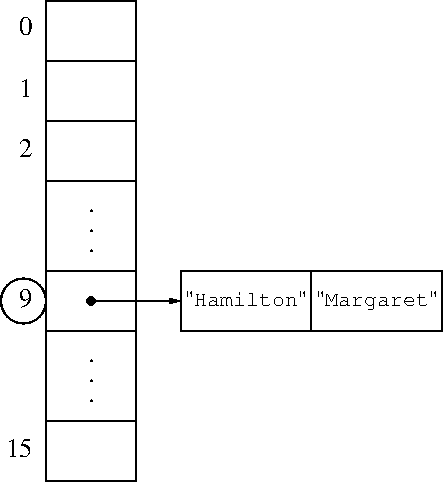
Okay, 27 slides in and we finally get to hashes! How do they work?
The basic idea is simple: We want to associate the data Margaret
with the key Hamilton. We will store everything in an array,
because arrays are fast and simple. Say the array has 16 elements.
We use some method to map the key Hamilton to an array index between
0 and 15.
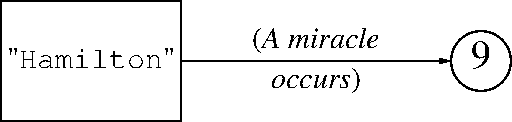
Then we store the key and the value in that array slot. The mapping is constant time. The array storage is constant time. Voilà!
Of course, I left out some crucial details. Fixing the details reduces the fetch and store performance to only O(log n). We'll see why in a minute.
There are at least three obvious problems, and perhaps some not so obvious. I didn't say how you map a string key to an array index; how is this done?
What if two keys map to the same index? There are only 16 indices, and rather more than 16 strings, so the problem will come up sooner or later.
And since there are only 16 slots, and rather more than 16 strings, what do you do when the array becomes full?
Happily, there are several good answers to all of these questions, and none of the answers is too hard.
The hash function is the function that takes a string and maps it to the index of the array slot it will be stored in.
David Albert said he was glad I was talking about this because choosing a hash function always seemed to him like a giant mystery. And it is, there's a huge amount of weird stuff that goes into it. But the basic principle is totally simple: When you choose the array slot that a key goes into, you want to choose it at random, because if you choose it at random you get optimal performance. (This is a theorem.) So in practice all hash functions are variations of the following method:
Take your favorite pseudo-random number generator. Seed it using the key. Extract a random number from it. You need a number between 0 and 15 so divide by 16 and take the remainder. That's the index.
That's it, that's the big mystery.

Some people spend a lot of time and effort tuning their pseudo-random number generators to maybe have better outcomes for key sets that maybe appear frequently in the real world. I have my doubts about the usefulness of this. I've never seen any of these people do a careful study of what kinds of hash keys are actually common.
It's really easy to make a claim of the form
Hash function H produces 14% fewer collisions on data of type X
and I have heard many such claims, all very credible. But that's not really useful unless you also make a bunch of claims of this type:
Data of type X appears as input to 7% of all real-world programs. Furthermore, we found that H only slowed down hash performance in the other 93% of real-world programs by only 1%.
Those latter claims are very, very difficult to support.
Questions about hash performance now come down to questions about what happens when you throw a bunch of balls (the keys) at random into a bunch of bins (the slots, also called buckets). This is known as the balls-in-bins problem, and it's well-studied because hashing is important. The crucial basic result is that if you throw about n balls into about n bins, then, with extremely high probability, the bin with the most balls will have only around log n of them. Without this, hashing wouldn't work.
When two keys want to go into the same bucket, that's called a collision, and we have to do something about it.
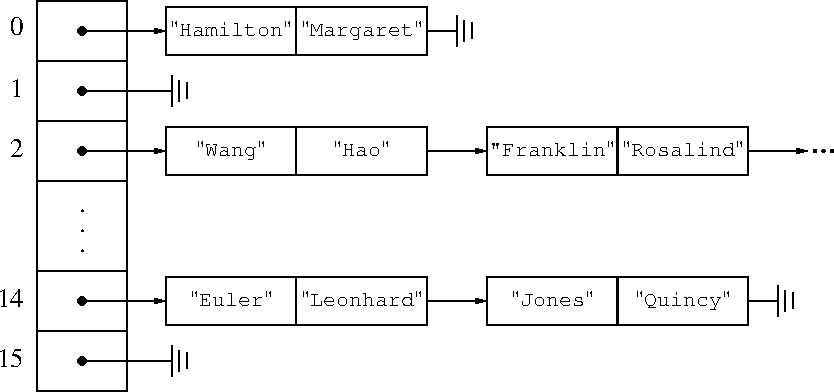
There are several ways to handle collisions. One of the most common, used in Perl, is called chained hashing: instead of storing one key and value per bucket, store a list. If you get a collision, add the new key and value to the front of the list.
The worst-case fetch and store time is now O(n), because all the keys and values might end up in the same bucket. But you were choosing the buckets at random, so the probability of this occurring is insignificant, it's like flipping a coin and getting a hundred heads in a row. The overwhelmingly likely behavior is that the longest list has length O(log n) (that's the crucial basic result from slide 30) and then the fetch and store times are only O(log n).
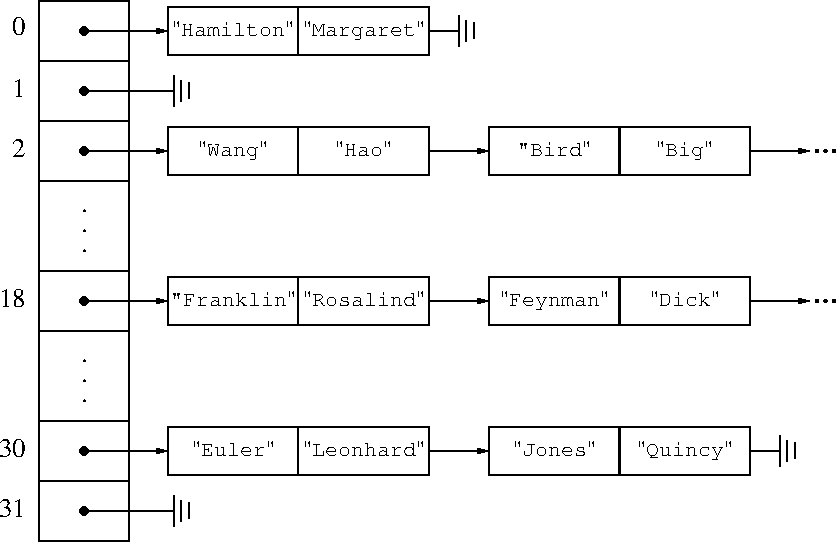
Of course, once you put enough items into the hash, the lists will get long and you are back to O(n) time. If you put 16 million items into a 16-bucket hash, at least one bucket has a million items in it. So when the hash starts to get full, Perl creates a new hash with twice as many buckets and redistributes the keys into it. Poof, all the lists are now half as long.
This sounds expensive, and it is. But it is also quite rare. Since the bucket array doubles every time, you only have to do it log n times, and the total cost of all the rebuildings is only O(n), which is a constant amount of time per item. So the cost over the lifetime of the hash is small.
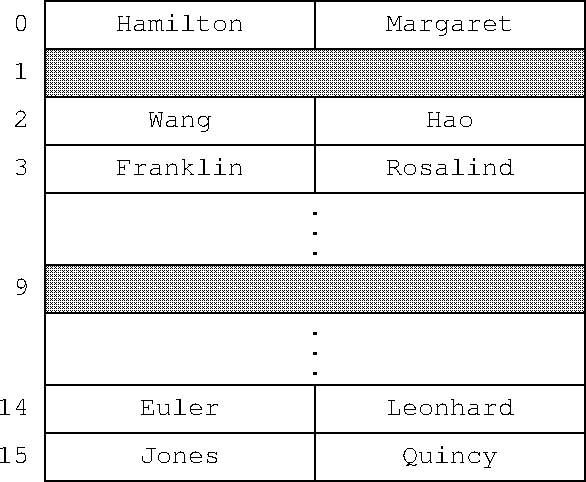
Python uses a complete different strategy to handle collisions. If it wants to insert an item into slot 2, and slot 2 is already full, it does a linear scan until it finds the next empty slot, and puts it there instead. On fetch, if it doesn't find what it does a linear scan on the following slots until it's successful or until it reaches and empty slot. If it falls off the bottom it continues from the top.
This also has O(n) worst-case behavior, since in the worst case it is a linear scan of the bucket array. But again, if the hash is not too heavily loaded, the probability of the worst case is insignificant. If the hash is half-full, then a slot is empty with probability ½, and Python only has to look at 2 slots on average before finding an empty one.
When the hash starts to get too full (someone at the talk checked the source, and found that “too full” means ⅔ full) then Python increases the bucket array (by a factor of 2 or 4) and redistributes the items. Again the amortized cost is low.
Deletion from a chained hash is easy; just delete the item from the corresponding linked list.
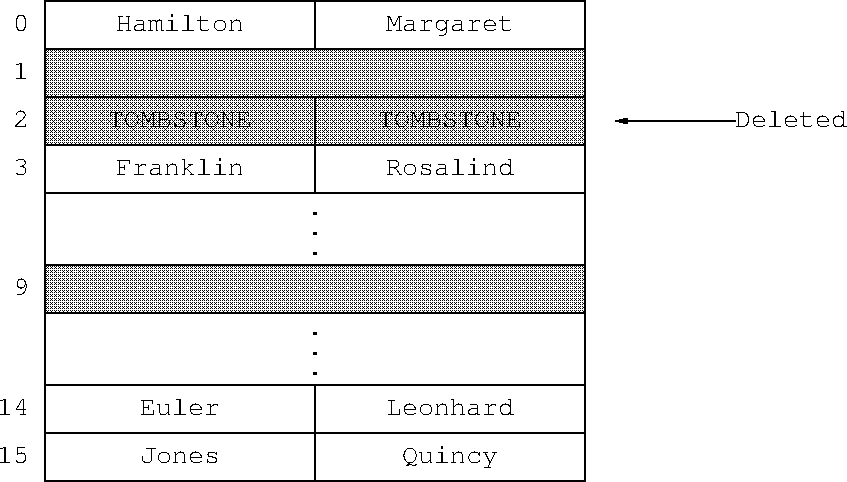
In open-addressing hashes it's a little more interesting. You can't simply delete the item, because that would leave an empty slot. For example, suppose Hao Wang and Rosalind Franklin both hash to slot 2, and Franklin was put in slot 3 instead. If we simply deleted Hao Wang, then a search for Franklin would fail, because it would start at the now-empty slot 2. So instead Python leaves behind what's called a “tombstone”: a marker that says that the slot was full, but was deleted. The tombstone won't stop the search for Franklin, which continues on to slot 3 as before. If another item is later inserted at slot 2, it can overwrite the tombstone. If the hash is rebuilt, all the tombstones can be discarded.
Many many thanks to the Recurse Center for inviting me to do a residency in the first place and to David Albert and Rachel Vincent for essential support while I was there.