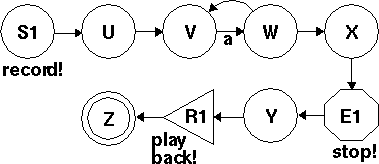
The third illustration on page 50 is missing a letter. There should be an a on the arrow from V to W, like this:

These diffs show how to add the . metacharacter to Regex.pm. We only need to add eight lines! If you want to try it yourself, don't peek!
Caution: This . isn't exactly like Perl's, because Perl's . doesn't match \n. It's a simple change to give it Perl's behavior.
The demo program illustrates an situation where Perl's built-in regular expressions take longer than Regex.pm to find that there's no match---a lot longer. How can this be? Is Regex.pm simply better?
No. The answer is that Regex.pm is worse, and that's why it's faster.
Huh?
Simple. Perl's built-in regexes have backreferences. Regex.pm doesn't. That lack of functionality enables Regex.pm to use a really super optimization that can speed things up a lot. However, the optimization makes it impossible to support backreferences. So Regex.pm is faster because it's less powerful.
This tradeoff is not a superficial thing, either. Regex.pm's algorithm is well-known and efficient. You might wonder if there is perhaps some way to extend it or modify it so that it works for regexes with backreferences too. The answer is that there probably isn't such an extension, for strong theoretical reasons.
Regexes with backreferences can be shown to be NP-Complete. This means, in practice, that there is no efficient algorithm known for computing whether or not such a regex matches, and that if there were such an algorithm, it would immediately translate into efficient algorithms for solving a huge class of other well-studied problems for which no efficient algorithms are known. This class of problems includes the famous Travelling Salesman problem, integer linear programming, the problem of recognizing whether or not a number is prime, and, in fact, any problem where you can efficiently check a proposed solution to see whather or not it is actually a correct solution.
Conversely, regular expression matching without backreferences is not NP-complete; there is a well-known, efficient algorithm for it, which is implemented by Regex.pm.
For more details, including a proof, see Regular Expression Matching is NP-complete.
Found an error, or have a remark? Send me mail.
Return to: Universe of Discourse main page | What's new page | Perl Paraphernalia | How Regexes Work