Reduction of GRAPH 3-COLORABILITY to Perl Regular Expression Matching

Credit: M-J. Dominus

The GRAPH 3-COLORABILITY Problem

A graph G=(V, E) is 3-colorable if there is a mapping f from the vertices V to {red, green, blue} such that f(u) = f(v) only if u-v is not an element of E. The graph 3-colorability problem is: Given a graph, is it 3-colorable?

Transformation to Regex Match

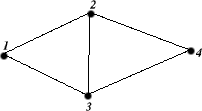
Let's represent the vertices of the graph as numbers between 1 and $V. We also suppose that we have an adjacency list for the graph. The adjacency list contains [u, v] if the graph contains an edge u-v. So for example, the following graph:

is represented as follows:

	$V = 4;
	@E = ([1,2], [1,3], [2,3], [2,4], [3,4]);

Construct a string as follows:

$string = (join "\n", (("rgb") x $V))
        . "\n:\n"
        . join "\n", (("rgbrbgr") x @E)
        ;

Now construct a regex as follows:

$regex =  '^'
       .  (join "\\n", (".*(.).*") x $V)
       .  "\\n:\\n" 
       .  (join "\\n", map {".*\\$_->[0]\\$_->[1].*"} @E)
       .  '$'
       ;

Now, the graph is 3-colorable if, and only if

	$string =~ /$regex/;

is true. If so, the backreference variables $1, $2, etc., contain the color assignments for the corresponding vertices of the graph.

Example

Suppose the graph is as depicted above. Then the value of $string is as follows: (The newlines are significant.)

	rgb
	rgb
	rgb
	rgb
	:
	rgbrbgr
	rgbrbgr
	rgbrbgr
	rgbrbgr
	rgbrbgr

and the value of $regex is:

	^.*(.).*\n.*(.).*\n.*(.).*\n.*(.).*\n:\n.*\1\2.*\n.*\1\3.*\n.*\2\3.*\n.*\2\4.*\n.*\3\4.*$

or, replacing the \n sequences with actual newlines for readability,

	^.*(.).*
	.*(.).*
	.*(.).*
	.*(.).*
	:
	.*\1\2.*
	.*\1\3.*
	.*\2\3.*
	.*\2\4.*
	.*\3\4.*$

The test $string =~ /$regex/ succeeds, so the answer to the question is yes. Additionally, the match operator assigns the values b, g, r, and b to the special variables $1, $2, $3, and $4, indicating that a 3-coloring of the graph has vertices 1 and 4 colored blue, vertex 2 colored green, and vertex 3 colored red. For an example of a no result, add [1,4] to the edge list.

Conclusion

Graph 3-colorability is NP-complete. If there were an efficient (polynomial-time) algorithm for computing whether or not a regex matched a certain string, we could use it to quickly compute solutions to the graph 3-colorability problem, and, by extension, to the knapsack problem, the travelling salesman problem, etc. etc.

Reference

Michael R. Garey and David S. Johnson: Computers and Intractibility: A Guide to the Theory of NP-Completeness. 1979, W.H. Freeman and Company. ISBN 0-7167-1045-5. pp 84--87, 191.

Return to: Universe of Discourse main page | What's new page | Perl Paraphernalia | NP-Completeness of Perl Regexes

mjd-perl-npc@plover.com